Chapter 01 Logic and Proofs 逻辑与证明

Part 02

Covering1.4 ~ 1.5

1. Predicate Logic 谓词逻辑

1.1. Predicate and Quantifiers 谓词和量词的概念

1.1.1. Predicate 谓词

A predicate (propositional function 命题函数) is a statement that contains variables.

Once the values of the variables are specified, the function has a truth value.

$P(x_1,x_2,...,x_n)$ n-place (n-ary) predicate n位谓词（n元谓词）

1.1.2. Quantifiers 量词

We need quantifiersto express the meaning of English words including all and some.

Universal Quantifier 全称量词

"For all"

∀

∀x P(x) is read as "For all x, P(x)" or "For every x, P(x)"

The universal quantification of P(x) create a proposition from a propositional function.

Existential Quantifier 存在量词

"There exists"

∃

∃x P(x) is read as "For some x, P(x)", or as "There is an xsuch that P(x)", or "For at least one x, P(x)."

Properties of Quantifiers 量词性质

Statement	When true?	When false?
$\forall x P(x)$	P(x) is true for every x.	There is an x for which P(x) is false.
$\exists x P(x)$	There is an x for which P(x) is true.	P(x) is false for every x.

Thinking about Quantifiers 深入理解量词

Loop 循环

When the domain of discourse is finite, we can think of quantification as looping through the elements of the domain.

To evaluate ∀x P(x) loop through all x in the domain
If at every step P(x) is true, then ∀x P(x) is true
If at a step P(x) is false, then ∀x P(x) is false and the loop terminates
To evaluate ∃x P(x) loop through all xin the domain
If at some step, P(x) is true, then ∃x P(x) is true and the loop terminates
If the loop ends without finding an xfor which P(x) is true, then ∃x P(x) is false

Even if the domains are infinite, we can still think of the quantifiers this fashion, but the loops will not terminate in some cases.

Conjunctions and Disjunctions 合取、析取

If the domain is finite, a universally quantified proposition is equivalent to a conjunction of propositions without quantifiers and an existentially quantified proposition is equivalent to a disjunction of propositions without quantifiers.

If U consists of the integers 1,2, and 3

$\forall x P(x)\equiv P(1)\wedge P(2)\wedge P(3)$

$\exists x P(x)\equiv P(1)\vee P(2)\vee P(3)$

Even if the domains are infinite, you can still think of the quantifiers in this fashion, but the equivalent expressions without quantifiers will be infinitely long.

Other Quantifiers 其他量词

Uniqueness quantifier 唯一性量词

$\exists!$ or $\exists_1$

∃!x P(x) means that P(x) is true for one and only one x in the universe of discourse.

Precedence of Quantifiers 量词优先级

The quantifiers ∀and ∃have higher precedence than all the logical operators.

Binding Variables 量词绑定

Bound Variable 约束的量词

a variable is bound if it is known or quantified.

Free Variable 自由的量词

a variable neither quantified nor specified with a value

All the variables that occur in a propositional function must be bound or set equal to a particular value to turn it into a proposition.

In the statement ∃x(x + y = 1), the variable x is bound by the existential quantification ∃x, but the variable y is free because it is not bound by a quantifier and no value is assigned to this variable. This illustrates that in the statement ∃x(x + y = 1), x is bound, but y is free.

However, this statement is not a proposition since y is undefined and we can't tell whether it is true or false.

1.2. Logical Equivalences Involving Quantifiers 涉及量词的逻辑等价式

Statements involving predicates and quantifiers are logically equivalent iff they have the same truth

x is not occuring in P

量词辖域的扩张

$\forall xP(x)\vee A\equiv\forall x(P(x)\vee A)$

$\forall xP(x)\wedge A\equiv\forall x(P(x)\wedge A)$

$\exists xP(x)\vee A\equiv\exists x(P(x)\vee A)$

$\exists xP(x)\wedge A\equiv\exists x(P(x)\wedge A)$

量词辖域的收缩

$\forall x(A\to P(x))\equiv A\to\forall xP(x)$

$\exists x(A\to P(x))\equiv A\to\exists xP(x)$

（下面的两个式子很重要）

$\forall x(P(x)\to A)\equiv\exists xP(x)\to A$

$\exists x(P(x)\to A)\equiv\forall xP(x)\to A$

1.3. Negating Quantified Expressions 量化表达式的否定

1.3.1. De Morgan’s Laws for Quantifiers 量词的德·摩根律

$\neg\forall xP(x)\equiv\exists x\neg P(x)$

$\neg\exists xP(x)\exists\forall x\neg P(x)$

Negation	Equivalent Statement	When is Negation True?	When False?
$\neg\exists x P(x)$	$\forall x\neg P(x)$	P(x) is false for every x	There is an x for which P(x) is true
$\neg\forall x P(x)$	$\exists x\neg P(x)$	There is an x for which P(x) is false	P(x) is true for every x

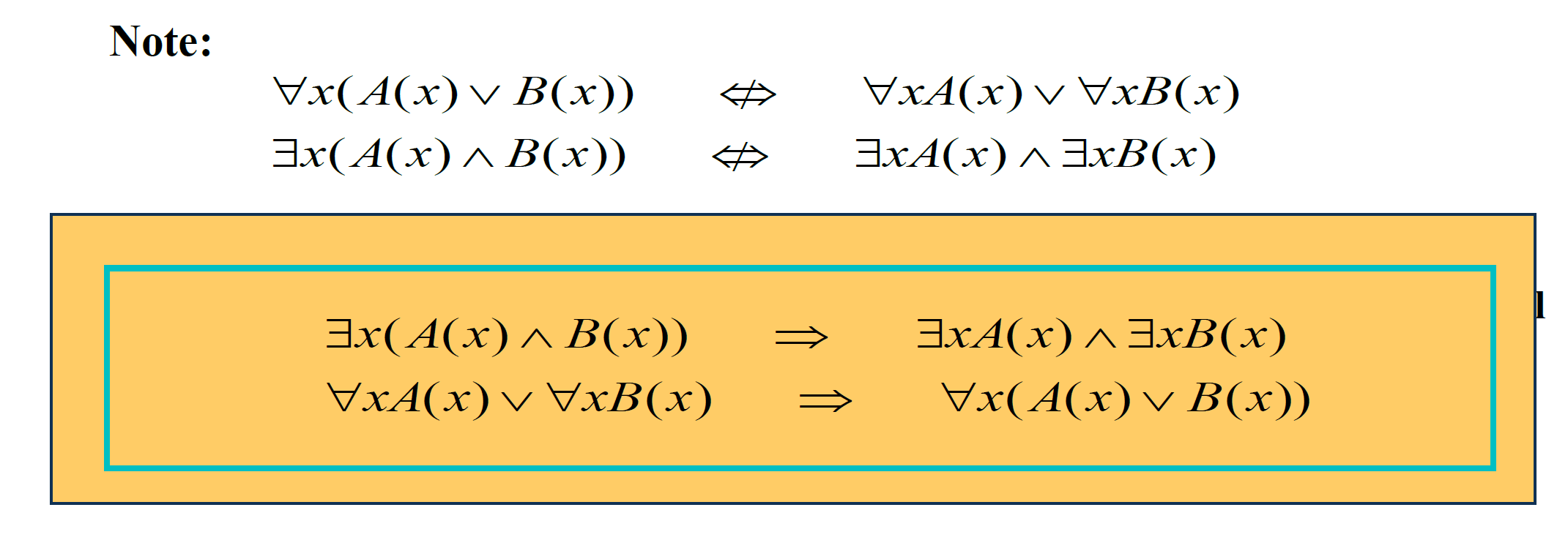
1.4. Translating from English into Logical Expressions

The very first step is to decide on the domain U.

Translate the following sentence into predicate logic “Every student in this class has taken a course in Java.”

First decide on the domain U.

Solution 1 If U is all students in this class, define a propositional function J(x) denoting “x has taken a course in Java” and translate as ∀x J(x).

Solution 2 But if U is all people, also define a propositional function S(x) denoting “x is a student in this class” and translate as ∀x (S(x)→ J(x)).

1.4.1. A Very Important Notice!!!

Every student in this class has taken a course in Java

if U is all people, also define a propositional function S(x) denoting “x is a student in this class”

$\forall x(S(x)\wedge J(x))$ is not correct!!!

if there is one x that does not belong to this class, then the whole statement is false!
Some student in this class has taken a course in Java

if U is all people

$\exists x(S(x)\to J(x))$ is not correct!!!

if there is one x that does not brlong to this class, the the whole statement is true!

1.5. Premises and Conclusion 前提和结论

Lewis Carroll Example

An argument

“All lions are fierce.”
“Some lions do not drink coffee.”
“Some fierce creatures do not drink coffee.”

The first two are called premises（前提） and the third is called the conclusion（结论）.The entire set is called an argument（论证）.

One way to translate these statements to predicate logic

Let p(x), q(x), and r(x) be the propositional functions “xis a lion,” “xis fierce,” and “xdrinks coffee,” respectively. Domain of x: All creatures.

∀x (p(x)→ q(x))
∃x (p(x) ∧¬r(x))
∃x (q(x) ∧¬r(x))

Later we will see how to prove that the conclusion follows from the premises.

2. Nested Quantifiers 嵌套量词

2.1. Definition 定义

Two quantifiers are nested if one is within the scope of the other.

e.g. $\forall x\exists yC(x,y)$

2.2. Translating from Nested Quantifiers into English

Translate the statement $\forall x(C(x)\wedge \exists y(C(y)\wedge F(x,y)))$ into English, where C(x) is "x has a computer," F(x,y) is "x and y are friends," and the domain for both x and y consists of all students at ZJU.

Solution

Use variables in the translatint result (Easy and clear)

For every student x at ZJU, x has a computer or there is a student y such that y has a computer and x and y are friends.

Understand the meaning and report it in English

Every student at ZJU has a computer or has a friend who has a computer.

2.3. Translating English into Logical Expressions Involving Nested Quantifiers

Express the statement “Everyone has exactly one best friend” as a logical expression with a domain consisting of all people

Solution

Rewrite the original statement as For every person x , x has exactly one best friend.

There is a person y who is the best friend of x, and furthermore, that for every person z, if z is not y, then z is not the best friend of x.

Let B(x, y) be the statement y is the best friend of x.

$\forall x\exists y\forall z(B(x,y)\wedge((z≠y)\to\neg B(x,z)))$

2.4. The Order of Quantifiers 量词顺序

The order of nested quantifiers matters if quantifiers are of different types

e.g.

$\forall x\forall yP(x,y)\equiv\forall y\forall xP(x,y)$

However

$\exists x\forall yP(x,y)$ is not the same as $\forall y\exists xP(x,y)$

Explanation

Assume P(x,y) denote "x loves y", where the domain for variables x and y consists of all people

$\exists x\forall yP(x,y)$ --> There is someone who loves everyone.

$\forall y\exists xP(x,y)$ --> Everybodyi s loved by somebody.

2.5. Negating Nested Quantifiers 嵌套量词的否定

Negating nested quantifiers by successively applying the rules for negating statements involving a single quantifier