Part 01 Set

Covering2.1 ~ 2.2

1. Set 集合

1.1. Basic 基本属性

1.1.1. Definition 定义

A set is an unordered collection of objects.

集合是对象的一个无序聚集。

Note:

• The Order of elements does not matter {1, 2, 3} = {3, 2, 1}
• Repetition of elements does not matter {1, 1, 2, 3, 3} = {1, 2, 3}

The objects in a set are called the elements（元素）, or members（成员）, of the set.

A set is said to contain（包含） its elements.

Note:

1. Uppercase letters are usually used to denote sets, and lowercase letters are usually used to denote elements of sets.

2. a ∈ A: a is a member (an element) of the set A

   a ∉ A: a is not an element of the set A

1.1.2. Description 描述方法

Roster Method 花名册法

listing all its members between braces

e.g. S = {a, b, c, d}

Brace Notation with Ellipses 省略号记法

Sometimes the roster method is used to describe a set without listing all its members. Some members of the set are listed, and then ellipses (. . .) are used when the general pattern of the elements is obvious.

e.g. The set S of positive integers less than 100 can be denoted by S = {1, 2, 3, . . . , 99 }

Set Builder 构造器

We characterize all those elements in the set by stating the property or properties they must have to be members.

e.g. {x | x is an odd positive integer less than 10}

Truth Sets 真值集

Given a predicate P, and a domain D, we define the truth set of P to be the set of elements x in D for which P(x) is true.

The truth set of P(x) is denoted by {x ∈ D | P(x)}.

1.1.3. Venn Diagrams 文氏图

• In Venn diagrams, the universal set U is represented by a rectangle.
• Inside this rectangle, circles or other geometrical figures are used to represent sets.
• Points are used to represent the particular elements of the set.

1.2. Property 性质

1.2.1. The Relations Between Two Sets 集合间的关系

Subset 子集

$A\subseteq B\Leftrightarrow\forall x\in A\to x\in B)$

For any set A

• $\phi\subseteq A$

• $A\subseteq A$

Equal 相等

$\begin{aligned}&A=B\\\Leftrightarrow&\forall x[(x\in A\to x\in B)\wedge(x\in B\to x\in A)]\\\Leftrightarrow&(A\subseteq B)\wedge(B\subseteq A)\end{aligned}$

To show that two sets A and B are equal, show that A ⊆ B and B ⊆ A.

Proper subset 真子集

$\begin{aligned}&A\subset B\\\Leftrightarrow&\forall x(x\in A\to x\in B)\wedge\exists x(x\in B\wedge x\notin A)\\\Leftrightarrow&(A\subseteq B)\wedge(A\ne B)\end{aligned}$

1.2.2. The Size of a Set 集合的大小

Let S be a set. If there are exactly n distinct elements in S where n is a nonnegative integer, we say that S is a finite（有限的） set and that n is the cardinality（基数） of S.

Notation: |S| -> the cardinality of S

e.g. Let A be the set of odd positive integers less than 10. Then |A| = 5.

​ |∅| = 0

A set is said to be infinite（无限的） if it is not finite

e.g. The set of positive integers is infinite

1.2.3. Power Set 幂集

Given a set S, the power set of S is the set of all subsets of the set S.

Notation: P(S) -> the power set of S

Note:

1. |S|=n implies |P(S)| = $2^n$
2. S is finite and so is P(S)
3. $x\in P(S)\Rightarrow x\in S（此处x是一个集合）\\x\in S\Rightarrow\{x\}\in P(S)（此处x是一个元素）\\S\in P(S)$

e.g.

What is the power set of the empty set? What is the power set of the set {∅}?

The empty set has exactly one subset, namely, itself. Consequently, P(∅) = {∅}. The set {∅} has exactly two subsets, namely, ∅ and the set {∅} itself. Therefore, P({∅}) = {∅, {∅}}.

A good way to check is to make sure |P(S)| = $2^n$

1.2.4. Cartesian Products 笛卡尔积

Tuple 元组

The ordered n-tuple（有序n元组） (a1, a2, . . . , an) is the ordered collection that has a1 as its first element, a2 as its second element, . . . , and an as its n-th element.

In particular, ordered 2-tuples are called ordered pairs（序偶）

$(x,y)=(u,v)\Rightarrow(x=u)\wedge(y=u)$

If $x\ne y$, then $(x,y)\ne(y,x)$

The Cartesian product of A and B, denoted by A × B, is the set of all ordered pairs (a, b), where a ∈ A and b ∈ B.

$A\times B = \{(a, b) | a\in A\wedge b\in B\}$

$A_1\times A_2\times· · ·\times A_n = \{(a_1, a_2, . . . , a_n) | a_i\in A_i\ for\ i = 1, 2, . . . , n\}$

Note:

If |A|=m, |B|=n, then |A×B|=|B×A|=mn

A×B≠B×A

A×∅ = ∅×A = ∅

1.3. Set Operations 集合运算

1.3.1. Intersection 交集

$A\cap B=\{x|x\in A\wedge x\in B\}​$

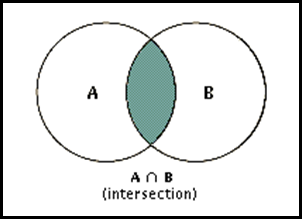
Two sets are called disjoint if their intersection is the empty set, namely $A\cap B = \empty$

Generalized Intersections 拓展的交集

$A_1\cap A_2\cap...\cap A_n=\bigcap_{i=1}^{n}A_i$

1.3.2. Union 并集

$A\cup B=\{x|x\in A\vee x\in B\}​$

The cardinality of the union of two finite sets:

$|A\cup B|=|A|+|B|-|A\cap B|$

Generalized Unions 拓展的并集

$A_1\cup A_2\cup...\cup A_n=\bigcup_{i=1}^{n}A_i$

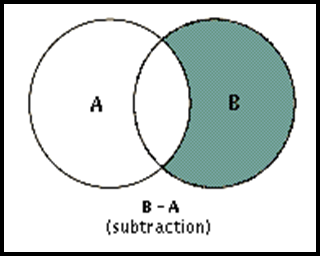
1.3.3. Difference 差集

$A-B=\{x|x\in A\wedge x\notin B\}$

1.3.4. Complement 补集

$\overline{A} = {x\in U | x\notin A}$

(U is the universal set)

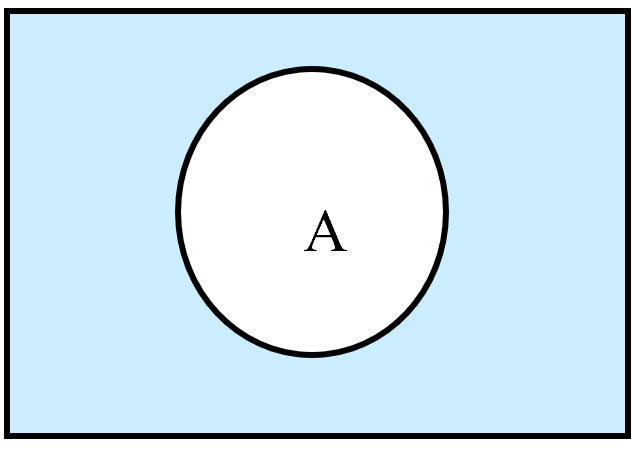
Note:

$A-B=A\cap\overline{B}$

1.3.5. Symmetric Difference 对称差分

$A\oplus B=(A\cup B)-(A\cap B)$

1.4. Set Identities 集合恒等式

1.4.1. Ways to Prove Set Identities 集合恒等式的证明方法

I. Show that A ⊆ B and that B ⊆ A

New and important

II. Use logical equivalences to prove equivalent set definitions

Easy but tedious

III. Use a membership table

Like truth tables

IV. Use previously proven identities

Like ≡

1.5. Computer Representation of Set 集合的计算机表示

Using bit strings to represent sets

1. Specify an arbitrary ordering of the elements of U, for instance $a_1,a_2,...,a_n​$
2. Represent a subset A of U with the bit string of length n, where the i-th bit is 1 if $a_i$ belongs to A and is 0 if $a_i$ does not belong to A.
3. Thus, Union -> bitwise OR Intersection -> bitwise AND

Example:

Let U ={1, 2, 3, 4, 5,6,7,8,9}, A={1, 2, 3, 4, 5}, B= (1, 3, 5, 7, 9).

The bit string for the set A: 11 1110 000

The bit string for the set B: 10 1010 101