Part 01 The Basic of Counting 计数基础

covering 6.1、6.3、6.4

1. Basic Counting Principles 基本计数原理

1.1. The Sum Rule 加法原理

If a first task can be done in $n_1$ ways and a second task in $n_2$ ways, and if these tasks cannot be done at the same time, then there are $n_1+n_2$ ways to do one of these tasks.

1.1.1. Phrased in terms of sets

If S and T are two disjoint finite sets, then the number of elements in the union of these sets is the sum of numbers of elements in them, namely $|S\cup T|=|S|+|T|$

Note:

If S and T have common elements, then we should use the inclusion-Exclusion principle (Subtraction Rule).

1.1.2. The extended version of the sum rule

We can extend the sum rule to more than two tasks.

Suppose that the tasks $T_1,T_2,…,T_m$ can be done in $n_1,n_2,…,n_m$ ways, respectively, and no two of these tasks can be done at the same time. Then the number of ways to do one of these tasks is $n_1+n_2+…+n_m$.

$|A_1\cup A_2\cup...\cup A_n|=|A_1|+|A_2|+...+|A_n|$

($A_i\cap A_j=\emptyset(i\neq j,\ i,j=1,2,…,n)$)

1.2. The Product Rule 乘法原理

Suppose that a procedure can be broken down into two tasks. If there are $n_1$ ways to do the first task and $n_2$ ways to do the second after the first task has been done, then there are $n_1n_2$ ways to complete the procedure.

1.2.1. Phrased in terms of sets

If S and T are finite sets, then the number of elements in the Cartesian product of these sets is the product of the number of elements in each set, namely $|S\times T|=|S|\cdot|T|$

1.2.2. The extended version of the product rule

$|A_1\times A_2\times...\times A_n|=|A_1||A_2|...|A_n|$

1.3. Subtraction Rule 减法原理

Also known as the Inclusion-Exclusion Principle

$|A\cup B|=|A|+|B|-|A\cap B|$

1.4. Division Rule 除法原理

There are n/d ways to do a task if it can be done using a procedure that can be carried out in n ways, and for every way w, exactly d of the nways correspond to way w.

这么说太抽象了，具体来说就是把平行、对称、对偶的情形除去，如果举一个例子的话就是环排列

1.5. Tree Diagrams 树状图

To use trees in counting, we use a branch to represent each possible choice. We represent the possible outcomes by the leaves.

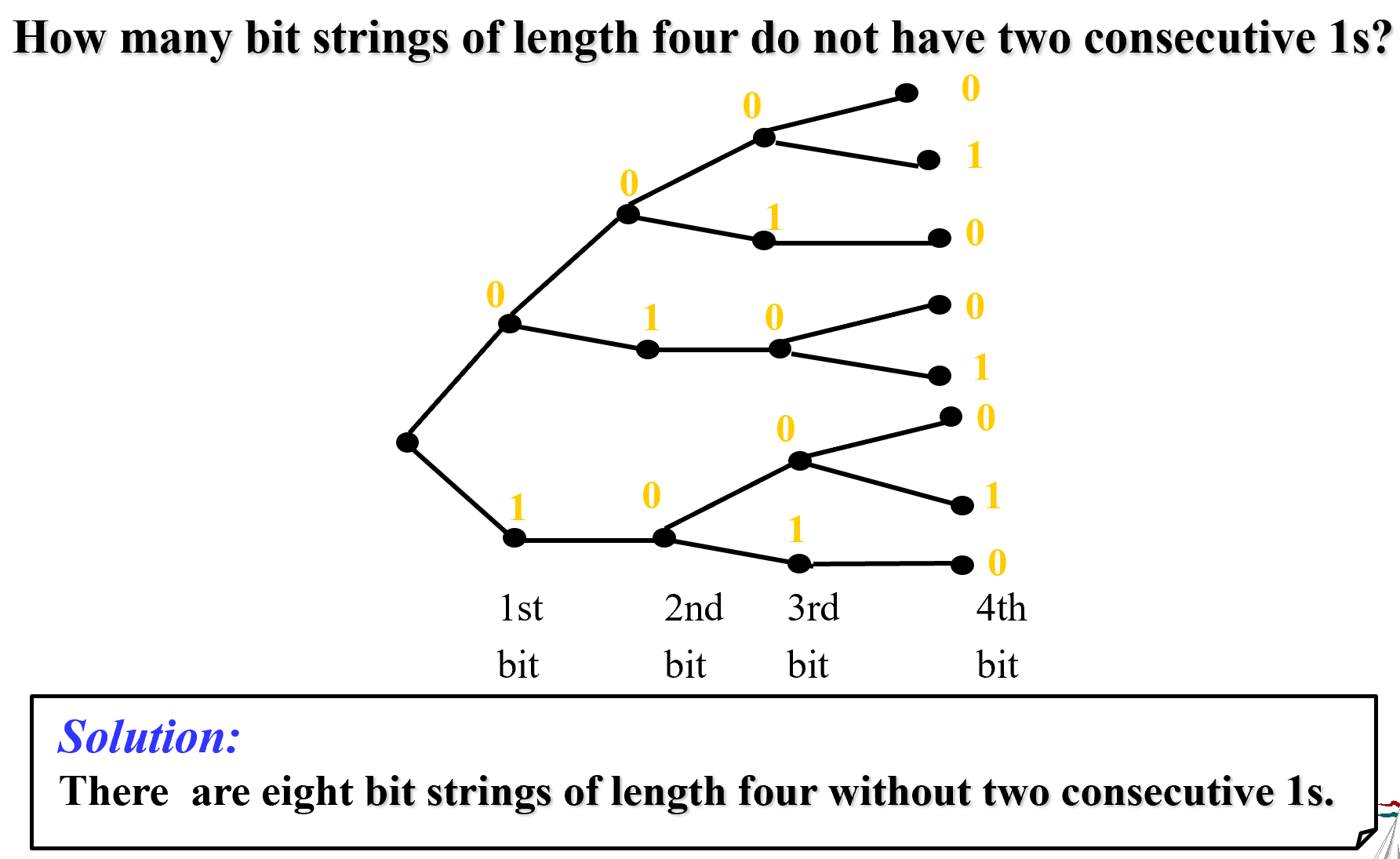
2. Permutations and Combinations 排列&组合

2.1. Permutations 排列

2.1.1. Definition 定义

A permutation of a set of distinct objects is an ordered arrangement of these objects.

An r-permutation is an ordered arrangement of r elements of a set.

Notation: $P(n,r)$

2.1.2. Theorem 定理

$P(n,r)=n(n-1)(n-2)...(n-r+1)=\frac{n!}{(n-r)!}$

This theorem can be proved by the product rule.

2.1.3. Phrased in terms of functions 函数表示

$B=\left\{b_{1}, b_{2}, \ldots, b_{r}\right\} \quad A=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\} \quad f : B \rightarrow A$

1. f is an injection from B to A $\Leftrightarrow$ an r-permutation of the set A
2. the number of injections from B to A $\Leftrightarrow$ P(n, r)

2.2. Combinations 组合

2.2.1. Definition 定义

An r-combination of elements of a set is an unordered selection of r elements from the set.

Note: An r-combination is simply a subset of the set with r elements.

Notation: $C(n, r)=\left( \begin{array}{l}{n} \\ {r}\end{array}\right)$

2.2.2. Theorem 定理

$C(n,r)=\frac{n !}{r !(n-r) !}=n(n-1)(n-2) \dots(n-r+1) / r !$

2.2.3. Phrased in terms of functions 函数表示

$A=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}, B=\{0,1\}, f : A \rightarrow B$

f is the function from A to B such that the image of r elements in A is 1 $\Leftrightarrow$ An r-combination of A. $C(n, r)=|\{f|f : A \rightarrow B \wedge r=|\{a|a \in A\wedge f(a)=1\}|\} |$

2.2.4. Corollary 推论

$C(n,r)=C(n,n-r)$

2.3. Combinatorial Proofs 组合证明

A combinatorial proof of an identity is a proof that uses one of the following methods.

2.3.1. Double Counting Proof 双计数证明

A double counting proof uses counting arguments to prove that both sides of an identity count the same objects, but in different ways.

2.3.2. Bijective Proof 双射证明

A bijective proof shows that there is a bijection between the sets of objects counted by the two sides of the identity.

e.g. Prove $C(n,r)=C(n,n-r)$

Double Counting Proof

counting the possible sets $A$ is equivelent to counting the set $\overline{A}$

Bijective Proof

$A\to\overline{A}$ is a bijection from a set containing r elements to a set containing (n-r) elements

3. Binomial Coefficients 二项式系数

3.1. The Binomial Theorem 二项式定理

Let x and y be varaibles, and let n be a nonnegative integer, then we have $(x+y)^{n}=\sum_{j=0}^{n} \left( \begin{array}{l}{n} \\ {j}\end{array}\right) x^{n-j} y^{j}$

3.1.1. Corollary 1 推论 1

$\sum_{k=0}^{n} \left( \begin{array}{l}{n} \\ {k}\end{array}\right)=2^{n}$

(x = y = 1 or use combinatorial proof)

3.1.2. Corollary 2 推论 2

$\sum_{k=0}^{n}(-1)^{k} \left( \begin{array}{l}{n} \\ {k}\end{array}\right)=0$

(x = 1, y = -1)

Note:

By this corollary, we have $> \left( \begin{array}{l}{n} \\ {0}\end{array}\right)+\left( \begin{array}{l}{n} \\ {2}\end{array}\right)+\left( \begin{array}{l}{n} \\ {4}\end{array}\right)+\ldots=\left( \begin{array}{l}{n} \\ {1}\end{array}\right)+\left( \begin{array}{l}{n} \\ {3}\end{array}\right)+\left( \begin{array}{l}{n} \\ {5}\end{array}\right)+\ldots >$

3.1.3. Corollary 3 推论 3

$\sum_{k=0}^{n} 2^{k} \left( \begin{array}{l}{n} \\ {k}\end{array}\right)=3^{n}$

(x = 1, y = 2)

3.2. PASCAL’S Identity 帕斯卡恒等式

Let $n$ and $k$ be positive integers with $k\leq n$, then $\left( \begin{array}{c}{n+1} \\ {k}\end{array}\right)=\left( \begin{array}{c}{n} \\ {k-1}\end{array}\right)+\left( \begin{array}{l}{n} \\ {k}\end{array}\right)$

Proof:

Assume we have a set $A=\left\{x, a_{1}, a_{2}, \cdots, a_{n}\right\}$

The left side means the number of subsets of size k from set A

The right side counts this in another way:

1. the subsets that contain x $\left( \begin{array}{c}{n} \\ {k-1}\end{array}\right)$
2. the subsets that don’t contain x $\left( \begin{array}{l}{n} \\ {k}\end{array}\right)$

3.2.1. Pascal's Triangle 帕斯卡三角形

3.3. Vandermonde’s Identity 范德蒙德恒等式

Let m, n and r be nonnegative integer with r not exceeding either m or n, then $\left( \begin{array}{c}{m+n} \\ {r}\end{array}\right)=\sum_{k=0}^{r} \left( \begin{array}{c}{m} \\ {r-k}\end{array}\right) \left( \begin{array}{l}{n} \\ {k}\end{array}\right)$

Proof: Assume A and B are two disjoint sets and |A|=m, |B|=n

The left side means the number of ways to pick r elements from $A\cup B$

The right side counts the same thing in another way: pick r-k elements from A and then k elements from B, where $0\leq k\leq r$, and sum all these numbers up

3.3.1. Corollary 4 推论 4

$\left( \begin{array}{c}{2 n} \\ {n}\end{array}\right)=\sum_{k=0}^{n} \left( \begin{array}{l}{n} \\ {k}\end{array}\right)^{2}$

(Let m = r = n, $\left( \begin{array}{c}{2 n} \\ {n}\end{array}\right)=\sum_{k=0}^{n} \left( \begin{array}{c}{n} \\ {n-k}\end{array}\right) \left( \begin{array}{l}{n} \\ {k}\end{array}\right)=\sum_{k=0}^{n} \left( \begin{array}{l}{n} \\ {k}\end{array}\right)^{2}​$)

3.4. Another Identity “无名”恒等式

Let n and r be nonnegative integer with $r\leq n$, then $\left( \begin{array}{l}{n+1} \\ {r+1}\end{array}\right)=\sum_{j=r}^{n} \left( \begin{array}{l}{j} \\ {r}\end{array}\right)$

Proof:

Use bit string

The left-hand side counts the bit strings of length (n+1) containing (r+1) 1s

The right-hand side counts the same objects by considering the cases corresponding to the possible locations of the final 1 in a string with (r+1) ones ($\sum_{k=r+1}^{n+1} \left( \begin{array}{c}{k-1} \\ {r}\end{array}\right)=\sum_{j=r}^{n} \left( \begin{array}{c}{j} \\ {r}\end{array}\right)$)